何故、我々が MAAT Digital 社の thEQorange を使用する必要があるのか

Learn More

この内容は MAAT Digital 社と共同で制作しております。

まずは以下の動画をご覧ください。

作ったスライドショーに表記ミスがいくつかあります。

動画では MAAT Digital の thEQorange の紹介と解説をしています。

https://www.maat.digital/theqorange

EQ の基礎概論

ここではまず、EQ の基礎理論を紹介したいと思います。

この理論は Analog EQ であろうが、Graphic EQ であろうが、古い、新しいにかかわらず、基本は同じ フィルター の理論を利用しており、Digital EQ に於いても同じです。

すべての Analog EQ、または Digital EQ、Graphic EQ、Parametric EQ にかかわらず、フィルタリングの概念に基づいています。

フィルタリング (Filtering)

漠然と我々は ハイパス・フィルター または ローカット・フィルター などを利用していて、フィルターを利用していますが、すべての EQ の基礎理論が フィルター によって成り立っています。

実は EQ の各バンドはすべて Filter という名前がついています。

ひとつ、ここでの説明が非常に曖昧な部分が動画上ではありまして、Band-Pass Filter と動画上では発言しておりますが Parametric EQ の場合、Peaking Filter (ピーキングフィルター) のほうが厳密には正しいです。

実は「フィルターというは EQ の基礎部分である」という説明をちょこっと説明しているポストが既にあります。そこでは突っ込んだ話はしていませんが、基礎であることをここで再確認してほしいと思います。

合わせて読みたい

EQ の概念とその向き合い方。

Category: DTM
2019/11/29

EQ を利用している人は人知れず、全てはフィルターを制御していた、ということを覚えてください。このフィルターには色々な種類と特性があります。

わざわざ乗せる内容ではないと思ったので式や詳細は ChatGPT 出力を引用、式が正しいかどうかは、正しい資料が手元にないため確認していません。

ローパスフィルター (Low-Pass Filter)

特性: 低い周波数成分を通過させ、高い周波数成分を減衰させるフィルターです。
用途: 高音域のノイズや不要な高周波成分をカットし、低音域を強調するのに使用されます。スピーカーやオーディオシステムのクロスオーバーにも使われます。
周波数応答

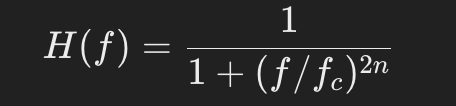
ハイパスフィルター (High-Pass Filter)

特性: 高い周波数成分を通過させ、低い周波数成分を減衰させるフィルターです。
用途: 低音のブーム音や不要な低周波ノイズを除去するために使われます。また、ボーカルや楽器の高音域を強調する際に利用されます。
周波数応答

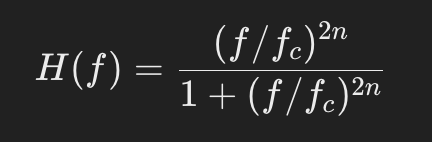
バンドパスフィルター (Band-Pass Filter)

特性: 特定の帯域の周波数を通過させ、その外の高周波と低周波を減衰させるフィルターです。
用途: 特定の帯域を取り出して、その周波数帯域だけを強調したいときに使用されます。例えば、無線通信や音響システムの調整に使われます。
周波数応答

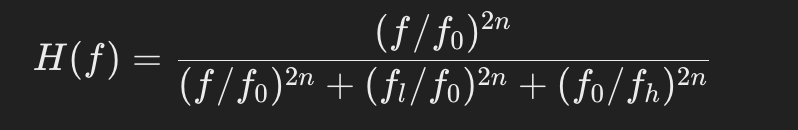
バンドストップフィルター (Band-Stop Filter)

特性: 特定の帯域を減衰させ、それ以外の帯域を通過させるフィルターです。
用途: ノッチフィルターとも呼ばれ、特定の周波数帯域のノイズやハム音を除去するために使用されます。例えば、50Hz や 60Hz の電源ノイズをカットするために使われます。
周波数応答

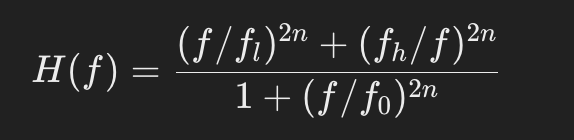
ピーキングフィルター (Peaking Filter)

特性: 特定の中心周波数をブーストまたはカットするフィルターです。狭い帯域に影響を与えるため、音質の微調整に適しています。
用途: ミキシングやマスタリングで、特定の周波数帯域を強調したり抑えたりするために使用されます。
周波数応答

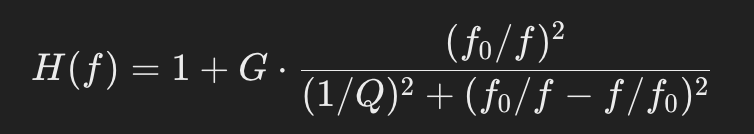
シェルビングフィルター (Shelving Filter)

特性: 低い周波数（ローファース）または高い周波数（ハイファース）をブーストまたはカットするフィルターです。特定の周波数を境に、ブーストやカットの効果が固定されます。
用途: トーンコントロールや音質調整で、全体的な低音や高音のバランスを調整するために使用されます。
周波数応答

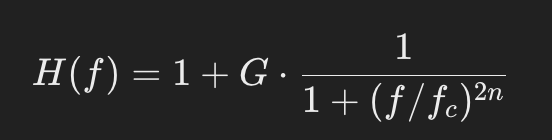
オールパスフィルター (All-Pass Filter)

特性: 全ての周波数を通過させますが、周波数ごとに位相を変化させるフィルターです。ゲインは変化しませんが、信号の位相シフトを引き起こします。
用途: 位相補正や位相のずれを調整するために使われ、特にステレオイメージの操作や複雑なフィルタリングシステムで役立ちます。
周波数応答

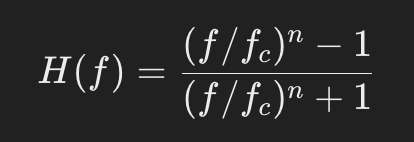
らしいです。僕は大学の数学を学びましたが、数式を他人にわかりやすく教えられる頭はないです。EQ を利用するうえで必要な知識としては、数学的な話より、実際のオーディオ信号に与える影響を熟知してください。

そしてオーディオ信号がフィルターを通過すると以下の応答が得られます。

周波数応答の変化

フィルターを通過すると特定の周波数成分が強調されたり、減衰したりします。これは、フィルターの 周波数応答 に基づいて決定されます。たとえば、ローパスフィルターは高周波成分を減衰させ、低周波成分を通過させるので、音の高域がカットされ、低域が残る音になります。逆に、ハイパスフィルターを通過すると低域が減衰し、高域が強調されます。

位相シフト

フィルターによっては 位相シフト（信号のタイミングの遅延）が発生します。位相シフトは、音の周波数ごとに異なるタイミングで信号が遅れる現象です。例えば、オールパスフィルター は周波数成分の振幅を変えずに位相だけをシフトさせます。位相シフトは、複数のフィルターを使用する場合や、特定の周波数で位相整合が必要な状況で重要な要素になります。

帯域幅のコントロール

フィルターを通過すると 帯域幅 がコントロールされます。たとえば、バンドパスフィルターでは、特定の周波数帯域のみが通過し、それ以外の帯域はカットされます。

Gain の変化

フィルターは特定の周波数帯域の Gain（振幅）に影響を与えます。ピーキングフィルターは、特定の周波数帯をブーストまたはカットします。

音の色付け

フィルターによっては 音の色付け（トーンの変化）が付与されることがあります。たとえば、アナログ機器のフィルターは、固有の非線形特性や倍音成分を加えることで、音に独特のキャラクターを与えることがあります。こうしたフィルターの音色の違いは、特にアナログフィルターや真空管機器などで顕著です。デジタルフィルターでも、アルゴリズムや設計によって微妙な音質の違いが生じることがあります。

時間領域での影響（パルス応答）

フィルターは信号の 時間領域での形状 にも影響を与えます。特に急激なカットオフを持つフィルター（高い次数のフィルター）は入力信号のエッジや過渡成分をなめらかにしたり、遅延を引き起こすことがあります。これにより、音のアタックが変化したり、音の鮮明さに影響を与えることがあります。時間領域での影響を評価する際は、インパルス応答 を調べることで確認できます。

遅延とフィルターの次数

フィルターの設計において、フィルターの 次数（オーダー）が高いほど、急峻なカットオフ特性が得られますが、その分遅延が増加します。これをグループ遅延（群遅延）と呼び、特にリアルタイム処理やライブサウンドでは重要な要素です。高い次数のフィルターを使うと、遅延が発生し、音の同期がずれることがあります。

非線形効果

アナログフィルターや一部のデジタルフィルターでは 非線形効果 が付与されることがあります。非線形フィルターは、入力信号のレベルや特定の条件下で動作が変化し、特定の倍音や歪み成分を加えることがあります。これにより複雑な倍音構成が加わることがあります。

EQ とは「等価交換」である

EQ は任意の周波数の振幅 (Gain) や特定の周波数以上、以外をカットすることができますが、副作用もあります。

位相の歪み（Phase Shift）

EQ のフィルターは特定の周波数をブーストやカットするだけでなく、信号の位相にも影響を与えます。特にアナログ EQ や一般的なデジタル EQ では 位相シフト（フェーズシフト）が発生します。これは音のタイミングにずれを引き起こし、音質に悪影響を与える可能性があります。

音の自然さの喪失

EQ で極端なブーストやカットを行うと、音の自然さ が損なわれることがあります。音が不自然に聞こえたり、特定の周波数が強調されすぎて、元の音の質感やバランスが失われてしまう可能性があります。

クリッピングや歪みのリスク

EQ で特定の周波数帯域を過剰にブーストすると、信号が過大入力（クリッピング）になり、デジタル歪み が発生することがあります。特にデジタルオーディオ環境では過度のブーストが信号レベルを超える原因となり、ノイズや歪みが混入します。

Q 値が高すぎると「耳障りな音」に

ピーキングフィルターで Q 値（帯域幅の狭さ）を極端に高く設定すると、特定の周波数が過度に強調され、音が 耳障り に感じられることがあります。これを俗に「ホンキートーン」と呼び、狭い範囲でのピークが鋭すぎると不快感を与える音になります。

音の厚みやパンチが失われる

EQ で特定の周波数帯域を大幅にカットすると、音の厚みやパンチ感が失われることがあります。特に低音域や中音域で過度にカットを行うと、音の力強さがなくなり、薄っぺらい音になることがあります。

不必要な帯域が強調される

EQ を使用して特定の周波数をカットした際に、逆に不必要な帯域が強調されることがあります。これは特定の周波数をカットすることで、別の周波数帯が相対的に強く感じられるようになる現象です。例えば、低音をカットしすぎると、高音域が過度に目立つようになり、バランスが崩れることがあります。

リソースの消費

デジタル EQ を多用すると、CPU やメモリなどのシステムリソースを消費します。特に、高精度のプラグインやリアルタイム処理が必要な場合、多くのトラックに EQ をかけるとシステムが負荷を受け、レイテンシーが発生したり、オーディオ処理が遅延することがあります。

マスキング効果の強調

EQ を適用することで、ある周波数帯が強調されると、その近くにある周波数帯が マスキング効果 によって聞こえにくくなることがあります。これは、ある帯域が強くなりすぎると、その隣接する帯域が抑え込まれてしまい、結果的にミックスが不明瞭になるという現象です。

フィルタリングアーティファクトの発生

デジタル EQ の場合、特定のフィルター設定によってアーティファクト（望ましくない音響効果）が発生することがあります。例えば、高い周波数でフィルタリングを行うと、エイリアシング やデジタルノイズが発生する可能性があります。また、強力なカットオフによって音に不自然な質感が加わることもあります。

非常に当たり前のことを記載していますが、今一度確認するために記載しています。

この中で、利用者が制御できない部分にフォーカスします。

位相シフト

位相シフトの量はフィルターの 周波数応答 に依存します。フィルターの 位相応答 は、周波数 ⨍ に対する位相シフト量を示すもので、フィルターの設計や種類に応じて変化します。フィルターの位相応答を数式で表すと次のようになります。

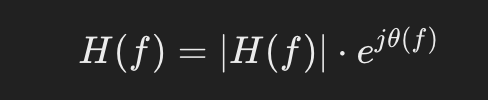
これに関連するデメリットとして、位相歪みがあります。

音の明瞭さや透明感の損失

位相歪みが発生すると、音のタイミングや波形が変わり、音の明瞭さや透明感 が損なわれます。これは、特に以下の点で顕著に現れます。

トランジェントのぼやけ: 位相が異なるシフトを受けることで、信号のアタックやトランジェント（瞬時の音の立ち上がり）がぼやけ、音のエッジが失われることがあります。これにより、特にパーカッシブな音やドラムなど、強いアタックを持つ音が不明瞭になることがあります。
高周波数の曇り: 高周波数成分は位相歪みに敏感で、音がくすんだように感じたり、全体のシャープさが失われることがあります。これにより、音が混濁し、聴きやすさが低下することがあります。

ステレオイメージのぼやけ

位相歪みは、ステレオイメージ にも大きな影響を与えることがあります。特に、以下のような影響が発生します。

定位の不明瞭化: ステレオ音場で左右チャンネルに異なる位相歪が生じると、音の定位がぼやけてしまい、音像が正確に定位しなくなることがあります。これにより、左右の音が不明瞭になり、音がどこから来ているのかが分かりにくくなります。
ステレオの広がりの損失: 位相歪みにより、音の定位や広がりが不均一になるため、ステレオイメージが狭く感じたり、音が前に出てこないことがあります。これにより、ミックス全体の奥行きや広がりが失われることがあります。

周波数干渉の悪化

位相歪みが発生すると、音の異なる周波数成分同士がタイミング的にずれることがあり、これにより 周波数干渉 が悪化することがあります。

打ち消し合いとブースト: 位相シフトが異なる周波数成分が重なることで、特定の周波数が強調されすぎたり、逆に減衰されてしまうことがあります。これにより、ミックス全体のバランスが崩れ、ある部分が不自然に強調されたり、重要な帯域が失われたりすることがあります。

音のタイミングの崩れ

位相歪みによって音のタイミングが変わるため、特に 複雑なミックス や 複数の楽器が絡む場面 では、音が微妙にタイミングを外れることがあり、全体的なパフォーマンスに影響を与えることがあります。

タイミングの不整合: 特定の周波数成分が位相シフトによって遅延すると、同じトラック内でも異なる音の部分が微妙にずれてしまい、ミックスが不安定に感じられることがあります。これにより、リズムやテンポの正確さが損なわれることがあります。

位相干渉による音質低下

複数の音源やトラックが 異なる位相シフト を受ける場合、位相干渉が発生し、音質が低下することがあります。

位相キャンセル: 位相歪みが発生すると、複数のトラックの音が干渉し、位相キャンセルが起こることがあります。これは、特定の周波数成分が互いに打ち消し合って、音が薄くなったり、部分的に消えてしまうことにつながります。
音のくぐもり: 位相干渉によって、特定の帯域が不明瞭になり、音がくぐもったように感じられることがあります。これにより、全体の音質が低下し、クリアさが失われる可能性があります。

フィルター処理後の波形の変形

位相歪みは、音の波形そのものを変形 させる可能性があります。特に、パルス信号や三角波、矩形波など、特定の形状を持つ波形に対して影響が大きいです。

波形の変形: 位相歪みによって波形の形が変わると、信号の元の特徴が損なわれ、音の特性が変わってしまいます。これは、特に正確な波形再現が求められるシンセサイザーの音や、アコースティック楽器の録音において問題になることがあります。

修正の難しさ

位相歪みが一度発生すると、それを後から 修正するのは非常に難しい 場合があります。位相を正確に補正するためには、高度なツールや複雑なプロセスが必要となることがあり、以下のような不便が生じます。

位相補正の複雑さ: 位相歪みを正確に補正するには、専門的な位相補正ツールを使用するか、フィルター設定を微調整する必要がありますが、これには多くの手間と経験が必要です。
音質への影響の回避が難しい: 特に最小位相フィルターでは、位相歪みを完全に避けることが難しいため、フィルター処理の選択肢が限られることがあります。

グループ遅延（群遅延）

グループ遅延（Group Delay）は、位相シフトの時間的影響を示す指標です。具体的には、信号全体がどの程度遅延するかを、各周波数成分ごとに評価するものです。グループ遅延は、位相応答の周波数微分として定義されます。

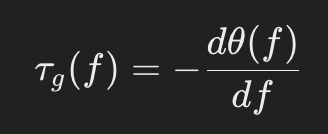
位相が周波数に対してどれだけ変化するか（すなわち、どれだけ位相シフトが周波数ごとに異なるか）を測ることで、信号がどの程度遅延するかを評価できます。一般的に、位相シフトが大きくなるほど、信号の遅延が増加します。特に、高周波成分ほど遅延が増大することが多いです。

これに関連するデメリットとして以下があります。

リアルタイム処理への影響

群遅延は、信号全体の時間的な遅れを引き起こすため、リアルタイム処理 が求められる状況では問題を引き起こします。具体的には、次のような影響があります。

パフォーマンスやライブ演奏: リアルタイムでのオーディオ処理が必要な場合（ライブパフォーマンスやスタジオでの録音中のモニタリング）、群遅延が長いと、音が遅れて聞こえることになり、ミュージシャンやパフォーマーにとって非常に不自然な体験になります。
レイテンシーの増加: 特に 線形位相 EQ を使用すると、全ての周波数成分に対して均一な遅延が発生します。この遅延は、通常のフィルターよりも大きいため、ミキシングやトラッキング時に レイテンシー が大きくなり、リアルタイム操作に支障が出る可能性があります。

音の時間的感覚の変化

群遅延が発生すると、音の時間的な位置関係が変わるため、トランジェント や アタック の感覚がぼやけることがあります。特に次のような影響があります。

トランジェントのぼやけ: 瞬間的な音、例えばドラムやパーカッションのアタック部分が遅延の影響を受け、鋭さや明瞭さ が損なわれることがあります。特に、急激な変化が重要な音源において、群遅延はその瞬間的なインパクトを弱めてしまうことがあります。
音のタイミングの崩れ: 複数のトラックや音源が異なるフィルター処理を受ける場合、異なる遅延がトラックごとに加わることで、全体的なタイミングの不整合が発生する可能性があります。これにより、ミックス全体が不明瞭になることがあります。

ミックスの不明瞭さ

群遅延が影響するのは、時間的な遅延だけではありません。音の 位相干渉 が発生することで、ミックス全体が不明瞭になることがあります。特に以下の点に影響が現れます。

ステレオイメージのぼやけ: 群遅延が音源の左右チャンネルに異なる影響を与えると、ステレオイメージが正確でなくなり、音像がぼやけることがあります。これにより、ステレオの定位感や広がりが失われる可能性があります。
周波数帯域の干渉: 周波数ごとに異なるグループ遅延が発生する場合、特定の周波数帯域に対してタイミングが不整合になることで、音が混濁し、特定の帯域が強調されすぎたり、逆に抑えられてしまうことがあります。

この 2 つの問題は通常の EQ では回避できません。

そこでデジタル領域では異なるアプローチを利用した EQ があります。

Linear Phase EQ

Linear Phase EQ はこれらのデメリットを解消した EQ となります。

Linear Phase EQ の特徴

位相の一貫性 Linear Phase EQ の最大の特徴は、全ての周波数成分に対して同じ位相シフトが適用されることです。これにより、信号のタイミングや波形が変わることがなく、音の 自然さ を保つことができます。例えば、複数の楽器トラックが混ざった際に、通常の EQ だと異なる帯域で異なる位相のずれが生じて音が濁ることがありますが、Linear Phase EQ ではそのような問題が発生しません。
位相歪みの回避 通常の EQ では、フィルタリングによって位相が周波数ごとに異なってシフトするため、特定の周波数が打ち消されたり強調されたりする 位相歪み が発生します。しかし、Linear Phase EQ では、これを回避し、周波数帯域全体で均一な位相を維持します。
タイムドメインでの遅延 Linear Phase EQ は位相を均一に保つために、フィルタリングの際にグループ遅延（群遅延）が発生します。これは、信号全体が一定の遅延を伴って処理されるということです。特に、リアルタイム処理やライブ環境では、この遅延が大きな問題になることがあります。遅延量は、使用する EQ のカットやブーストの度合い、フィルターのカーブによって変わります。

Linear Phase EQ のデメリット

遅延の増加: 遅延が発生するため、リアルタイム処理には不向きです。特に多くのバンドを使用した複雑なフィルタリングでは、遅延が目立つことがあります。録音時のモニタリングやライブでの使用では、タイミングのずれが発生しやすくなります。
CPU 負荷の増加: Linear Phase EQ は、通常の EQ と比べて 計算量が多いため、処理に必要なCPUリソースが増加します。特に高い解像度で使用する場合、DAWやプラグインの負荷が高くなることがあります。
音の人工的な変化: 一部のケースでは、Linear Phase EQ を使用した結果、音が 人工的 に感じられることがあります。特に極端なブーストやカットを行った際に、自然なサウンドではなくなることがあります。

Linear Phase EQ フィルター設計

Linear Phase EQ のフィルターは、位相特性を均一に保つために設計されています。これは、以下の特性に基づいています。

対称的なフィルタリング: Linear Phase EQ は、フィルターを設計する際に 対称的なフィルタリング を使用します。これにより、全ての周波数成分に対して均一な位相シフトが適用され、音質の透明感を保つことができます。
群遅延の管理: フィルターの設計により、各周波数帯域で同じ遅延が発生します。これにより、信号が同時に処理され、位相歪を最小限に抑えます。遅延量は、フィルターの設計や設定によって異なりますが、一般的に全体的な信号遅延が発生します。

Linear Phase EQ のフィルターは、FIR フィルター（有限インパルス応答フィルター）を使用していることが一般的です。FIR フィルターは、以下の特性があります。

線形位相特性: FIR フィルターは、適切に設計されることで、位相の均一性を保つことができます。これにより、全ての周波数が同じタイミングで到達し、音の透明感を維持します。
計算の複雑さ: FIR フィルターは、高い周波数分解能を持つため、設計には多くのサンプルが必要であり、計算量が増加します。これにより、CPU 負荷が高くなる場合があります。

Impulse Response

FIR フィルターの概念を知るためには IR（インパルス応答）について知る必要があります。

Impulse 信号とは

理論上は振幅無限大、時間幅無限小、積分 (ラプラス変換) すると 1 のデルタ関数

の現実的にはありえない関数のことです。

これをデジタルデータ上（DAW）で再現すると…

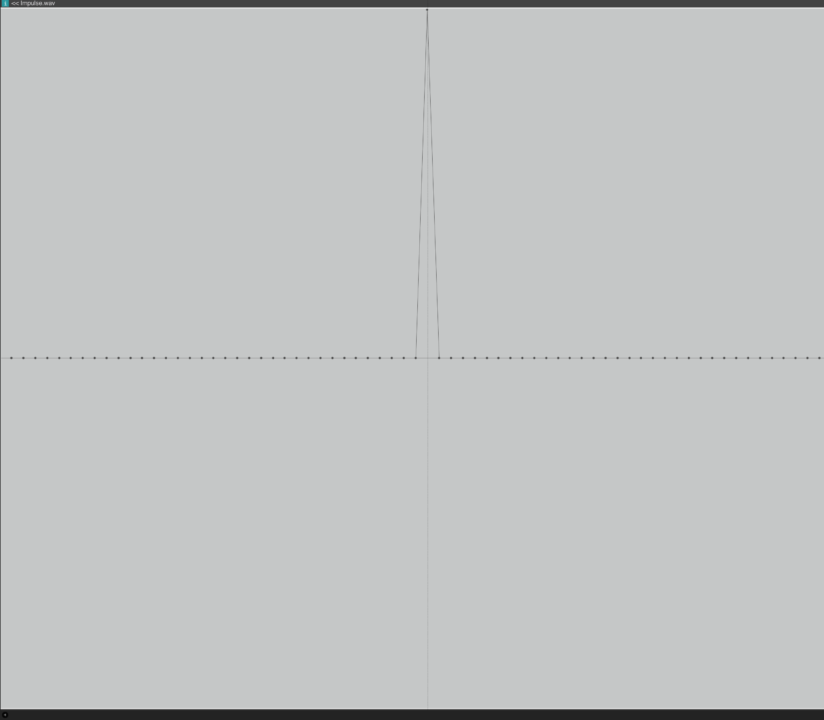
このような波形になる。

1 sample だけ 0 dBFS に到達し、あとはすべて 0 の波形である。

この波形の周波数特性を見ると…

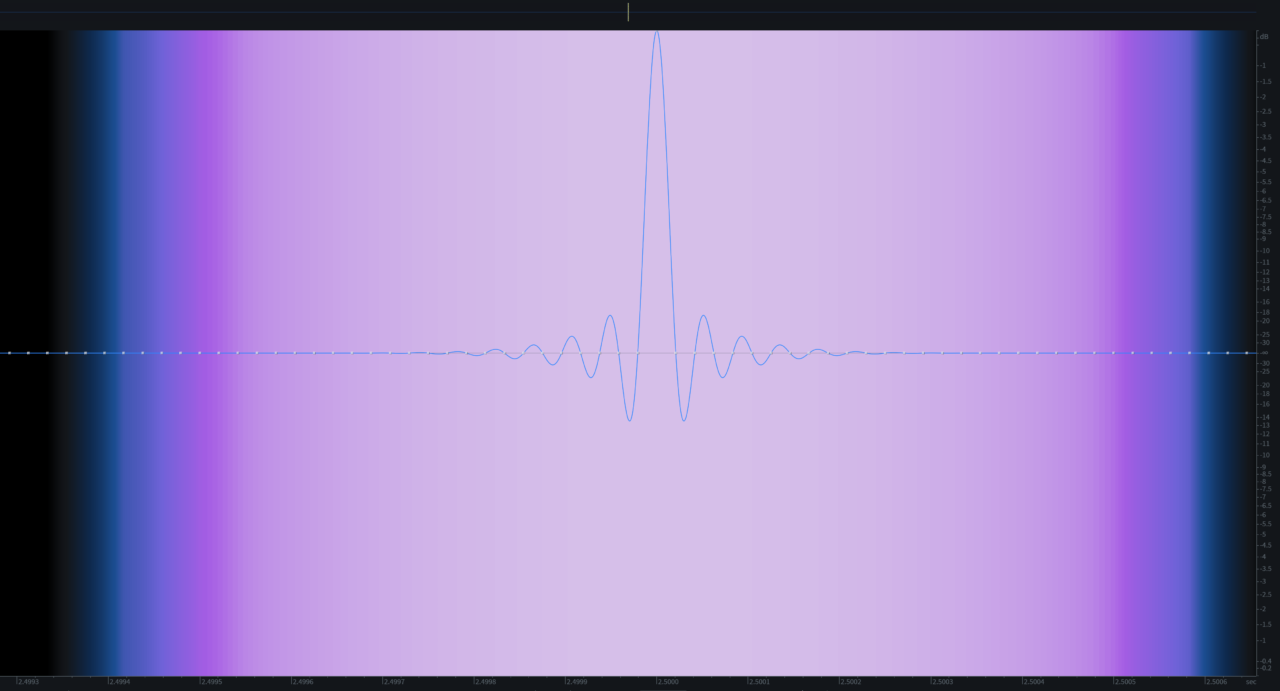
RX 上ではアナログ信号の復元表示をするため、このような波形になる。

これは何を意味するかというと、この Impulse 信号は ナイキスト以下のすべての周波数を含む波形 となる。

実際に Impulse Resonse を利用して畳み込み計算する場合は Tap 数で解像度が変わるお話なので詳細的な話は難しいお話ですが、ここではそこまで突っ込んで私が解説できません。

これはシステムに対してインパルスを入力するとその応答として安定して収束するのか、不安定になり発散するのか、いわゆるシステム そのものの特性 が現れます。これがインパルス応答（Impulse Response）です。

Impulse Response と伝達関数と周波数特性

Impulse Response は 1960 年代から利用されているもので特別、新しいものではありません。しかし、コンピュータで処理できるようになってから、オーディオミキシングで急速に利用が加速しました。

インパルス応答、伝達関数、および周波数特性は、線形時不変システム（LTIシステム）の解析において重要な概念であり、システムの動作を理解するために相互に関連しています。以下にそれぞれの定義と関係性を説明します。

インパルス応答（Impulse Response）

インパルス応答は、LTIシステムにおいて特定の入力（単位インパルス信号）に対する出力の応答を示します。デルタ関数（ディラックのデルタ関数）を入力として与えたときの出力信号を表します。

時間領域の特性: インパルス応答は、システムが時間的にどのように応答するかを示し、主に信号処理やフィルタリングの動作を理解するために用います。

伝達関数（Transfer Function）

伝達関数は、システムの出力と入力の関係を周波数領域で表すもので、ラプラス変換を用いて導出されます。

周波数領域の特性: 伝達関数は、システムの周波数特性を理解するための重要なツールであり、安定性や周波数応答の評価に使用されます。

周波数特性（Frequency Response）

周波数特性は、システムが異なる周波数成分に対してどのように応答するかを示すもので、伝達関数の周波数領域における評価結果です。

特性の表現: 周波数応答は、システムの振幅特性（どの周波数が強調または減衰されるか）と位相特性（信号の位相シフト）を示します。

関係性

これらの概念は、ラプラス変換やフーリエ変換を通じて相互に関連しています。

インパルス応答から伝達関数へ: インパルス応答のラプラス変換を取ることで、伝達関数を得ることができます。
伝達関数から周波数特性へ: 伝達関数を周波数領域で評価することで、周波数特性を得ることができます。
周波数特性からインパルス応答へ: 周波数応答の逆フーリエ変換を取ることで、インパルス応答を得ることができます。

インパルス応答と周波数特性は等価である

つまり、任意のインパルス応答を合成できるのであれば、周波数特性も合成できます。これを利用しているのが昨今の Digital EQ の基礎概論です。

動画上ではインパルス応答をフーリエ変換をすれば伝達関数がわかる的な説明ですが、インパルス応答からラプラス変換すると伝達関数がわかって、インパルス応答をフーリエ変換すれば周波数特性がわかる、伝達関数から計算で周波数特性がわかるし、周波数特性から振幅特性と位相特性も計算で得られます、的な話であり、インパルス応答 (時間領域) と伝達関数 (周波数領域) はフーリエ変換と逆フーリエ変換で互い行き来できる関係ということです。

役に立った数学の話 うさぎでもわかる信号処理

動画上では私も資料の理解度が低いためにインパルス信号をインパルスレスポンスといい間違えていることに気づいていませんし、インパルスレスポンスからフーリエ変換で伝達関数がわかると言っています。正しくはラプラス変換で伝達関数がわかり、伝達関数から周波数特性が得られ、インパルス応答のフーリエ変換で周波数特性がわかる、という話が正しいのでこちらで補完してください。

インパルス応答 (時間領域) をフーリエ変換すればそりゃ周波数領域へ変換できるし、周波数領域を逆フーリエ変換すればインパルス応答 (時間領域) に戻るって話です。これを利用して信号の合成を行うんですね。一旦元信号とインパルス応答を高速フーリエ変換してこの 2 つの関数を合成して最終的に時間領域 (音声波形) へ戻す的な話。

中身は数学の話でフーリエ変換と高速フーリエ変換は実際には指している自称は違うことだし、本当の変換は離散フーリエ変換 (DFT) であり、DFT (離散フーリエ変換) の計算を高速に行うアルゴリズムのことを「高速フーリエ変換」っていうらしくて、ややこしい。

※ このあたり、ラプラス変換とフーリエ変換の違いは周波数領域に゙関連する解なのか過渡現象に関連する解なのかの違いがあり、フーリエ変換はできないけどラプラス変換はできる関数である場合、その関数を一旦ラプラス変換したあとにフーリエ変換するという純粋数学の話が関連してきたり、インパルス応答でラプラス変換を行うのはフーリエ変換の変数に実部を加えることで指数関数による発散や減衰の性質を付加するため、らしく、実際の計算でラプラス変換を使うことはなく、高速フーリエ変換してから計算らしいので深くは突っ込みません。

個人的には深く理解していませんが、わかりやすい講義です。

以下は変換で得られる相互関係の図です。

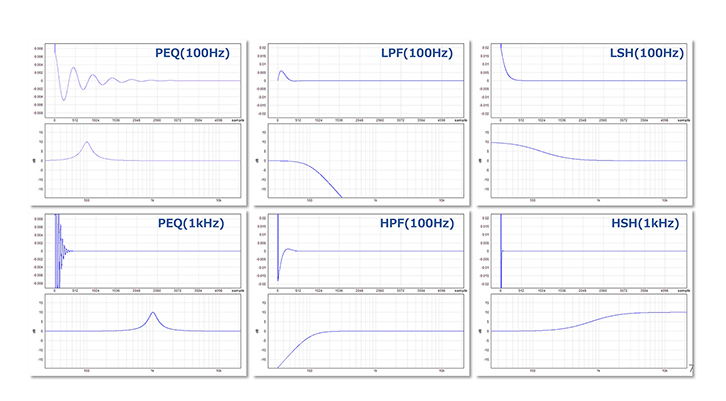
引用: https://www.yamaha-ss.co.jp/published-articles/journals-04.html

画像の通り、インパルス応答を利用すると EQ の振幅と位相応答を再現できるということ。これは YAMAHA さんが解説しています。嘘や間違っているとご意見がある人は YAMAHA さんへご連絡してください。

つまり、FIR フィルターというのはインパルス応答を利用したものということです。

FIR フィルター

インパルス応答について理解したら FIR フィルターについて総合的に見ていきましょう。

FIR フィルターの特性

安定性: FIR フィルターは常に安定であり、出力信号が無限大になることはありません。これは、有限のタップ数に基づく設計から来る特性です。
線形位相特性: FIR フィルターは、設計次第で線形位相特性を持つことができます。これは、すべての周波数成分が同じ遅延を受けるため、位相歪みが少なく、音質の保持に寄与します。
設計の柔軟性: FIR フィルターは、目的の周波数応答を得るために、タップ係数を自由に調整できるため、さまざまな応答特性（低域通過、高域通過、帯域通過など）を実現できます。

FIR フィルターの設計

窓関数法: 理想的な周波数応答を持つフィルターのインパルス応答を求め、窓関数を適用して有限の長さに制限します。
最小二乗法: 誤差を最小化するようにタップ係数を決定します。
周波数サンプリング法: 望ましい周波数応答をサンプリングし、それに基づいてタップ係数を決定します。

プリエコー

プリエコーは、信号の急激な変化の前に現れるエコーのような成分です。特に、トランジェントが発生した際に、その直前に過剰に応答することで生じます。

FIR フィルターの対称性: FIR フィルターは通常、対称的なタップ係数を持ちます。この特性により、信号の変化に対して遅延した応答が生じることがあります。
急激な信号変化への応答: 信号の立ち上がり部分やトランジェントに対して、フィルターが過剰に反応し、メインの信号の前にエコーのような成分が出現します。
音質の低下: プリエコーは、音声や楽器の明瞭さを損なうことがあり、特に急激な信号変化において不快に聞こえる場合があります。

ポストエコー

ポストエコーは、信号の急激な変化の後に現れるエコーのような成分です。メインの信号が出た後に続いて振動や残響が生じる現象です。

遅延した応答: FIR フィルターのインパルス応答が急激な信号変化に対して遅延し、メインの信号の後に振動が残ることで、ポストエコーが発生します。
フィルター特性: 特に高周波成分が強い場合、フィルターの特性によって過剰な応答が生じ、メインの信号に続いてエコーが現れることがあります。
音質の低下: ポストエコーも音質に影響を与え、特にトランジェントが強調されたり、他の音と混ざった際に不快に聞こえたりすることがあります。

プリンギング（プリリンギング）

プリリンギングは、信号の急激な変化、特にトランジェントの立ち上がり部分の前に現れる過剰な振動や残響です。フィルターがトランジェントの立ち上がりに対して遅延した応答を示すことで、元の信号の前にエコーのように聞こえる成分が生じる現象です。

FIRフィルターの対称性: FIR フィルターは通常、対称的なタップ係数を持ちます。この特性が急激な信号変化に対する応答を遅延させ、プリリンギングを引き起こします。
急激な信号変化: トランジェントが発生する際、フィルターはメインの信号が来る前に過剰に反応し、前方にエコーのような成分を生じさせます。
音質への影響: プリンギングは、音声や楽器の明瞭さを損ない、特にトランジェントの前に不快な振動を引き起こすことがあります。

ポストリンギング

ポストリンギングは、信号の急激な変化、特にトランジェントの立ち下がり部分の後に続く振動や残響です。メインの信号が出た後に現れる不必要な振動やエコーのような成分です。

遅延した応答: FIR フィルターが信号の変化に対して遅延した応答を示し、特に高周波数成分が強い場合に、メインの信号の後に振動が残ります。これがポストリンギングを引き起こします。
急激な周波数変化: フィルターの特性により、急激な周波数変化に対して過剰な応答が生じ、トランジェントの後にエコーのような成分が現れることがあります。
音質への影響: ポストリンギングも音質に影響を与え、特にトランジェントが強調されたり、他の音と混ざった際に不快に聞こえることがあります。

リンギングとエコーの問題は呼び方が違いのようで中身はほとんど一緒ですね。

対称性

線形位相＝対称性

実はフィルターの線形位相特性を保ちたい場合は フィルターは対称性 を持ちます。

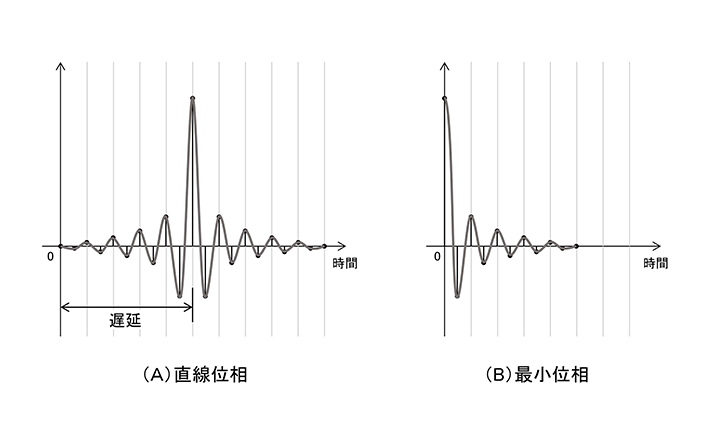
引用: https://www.yamaha-ss.co.jp/published-articles/journals-07.html

この対称性（線形位相）を保つためにデメリットである現象が起きると言っても過言ではありません。

従来の IIR フィルター

IIR フィルターは従来のデジタル EQ に利用されており、アナログ EQ のモデルはこちらで再現できます。

こちらは Minimum Phase EQ と呼ばれますが、最小位相のフィルターです。

フィルター構造: IIR フィルターは、フィードバックを使用して出力を生成します。このため、過去の出力信号が現在の出力に影響を与えます。一般的な構造には、バターワースフィルター、チェビシェフフィルター、エリプティックフィルターなどがあります。

特性

周波数特性: IIR フィルターは、特定の周波数帯域に対して急激なロールオフ（減衰）を実現できます。これは、比較的少ないタップ数で高い精度を持つフィルター特性を得ることができるため、計算効率が高いです。
安定性: IIR フィルターは、設計時に安定性を考慮する必要があります。フィルターの極（ポール）が単位円内に配置されていなければ、出力が発散する可能性があります。
レイテンシ: IIR フィルターは、遅延が比較的少ないため、リアルタイム処理に適しています。

利点

計算効率: IIRフィルターは、少ないタップ数で高い性能を持つため、計算リソースの消費が少なく済みます。これにより、プロセッサの負荷を軽減できます。
高い周波数特性: 急激な周波数応答が可能なため、特定の帯域を効果的にフィルタリングできます。

欠点

位相歪み: IIR フィルターは、位相応答が非線形であるため、位相歪が生じる可能性があります。これにより、信号の明瞭性が低下することがあります。
安定性の管理: IIR フィルターの設計では、安定性を確保するために注意が必要です。設計が不適切な場合、フィルターが発散する可能性があります。
リンギング: トランジェントに対して過剰に反応しやすいため、リンギングやプリエコーが発生することがあります。

thEQorange

やっとここまで来ました。正直 AI さんの引用ばかりでただのコンテンツ量稼ぎです。

Algorithmix の伝説的なオリジナル Linear Phase PEQ Orange

おそらく、この EQ について存在を知っている人は、ほぼ、いないと思います。

Dr. Christoph Musialik と Dr. Ulrich Hatje が共同創業者です。

Linear Phase PEQ Orange

価格は未だに € 1,190 って表記がある。

既に開発が終了しているオリジナルの EQ が存在し、開発元の Algorithmix との合意が成立、MAAT は 2017 年半ば開発を開始しました。

thEQorange は Forward-Backward Filter を利用している。

thEQorange は既存の再帰フィルター（つまり IIR フィルター）と Forward-Backward Filter を利用した周波数ドメインの Linear Phase EQ の仲間です。

Forward-backward 理論は、信号処理においてデータを前向き（順方向）と後向き（逆方向）の両方向で処理することにより、位相歪みを取り除き、ゼロ位相（位相遅れゼロ）のフィルタリングを実現する理論です。この理論の根幹は、信号を順方向に処理した後、逆方向に処理することで、フィルタの位相応答を相殺し、振幅応答を保ちながら位相歪みを打ち消す点にあります。

この理論には以下の特徴が含まれます。

ゼロ位相特性: 順方向と逆方向にデータをフィルタリングするため、各サンプルの処理が相殺され、結果として位相の遅れがゼロになる「ゼロ位相特性」が実現します。この特性により、波形の形状を維持しながらノイズや不要な成分を除去でき、特にピーク検出やエッジ検出など、位相歪みが問題となるアプリケーションに適しています。
安定性: この手法は一般に安定であり、順方向・逆方向の処理を組み合わせることにより、フィルタの安定性が保持されます。特に IIR フィルタにおいて安定な設計が容易になる利点があります。
利点と制約: Forward-backward フィルタは、過去のデータと未来のデータが両方必要なため、リアルタイム処理には向いていません。代わりにオフライン処理（すでに記録されたデータの後処理）で主に使用され、位相歪みのない高精度なフィルタリングが求められる場面で有用です。
フィルタリング効果の二乗: フィルタは前方向と後方向で二回適用されるため、フィルタの振幅特性は一度の適用に比べて二乗されます。これは、フィルタの特性を強調することになります。

Forward-backward フィルタの理論は、特に音響信号や画像データの処理に活用され、デジタル信号処理の分野で非常に重要な位置を占めています。この理論に基づくフィルタリングは、Butterworth フィルタや Chebyshev フィルタなどの IIR フィルタと組み合わせることが多く、信号を高精度に処理し、歪みのない出力が得られることから、多くのアプリケーションで標準的な手法として利用されています。

これだけ見ると、ほとんど FIR フィルターと特性は同じです。

Forward-Backward Filter

Daniel Weiss（現: Weiss Enginnering）の PEQ がこの Forward-Backward を利用した最初のオーディオ製品として発売されています。理論的には新しいものではありません。

理論的には線形位相の通常の再帰フィルター（IIR フィルタ）は存在しません。しかし、Forward-Backward 理論を併用すれば可能です。

これは保存されているオーディオデータであれば、適応できます。

線形位相＝対称性

という言葉を聞いたと思います。

つまりは位相特性の対称性のためにこの Foward-Backward Filter を利用すると考えてください。

※ 以下は簡単な図解であり、理解を深めるもので厳密な Filter の説明ではありません。

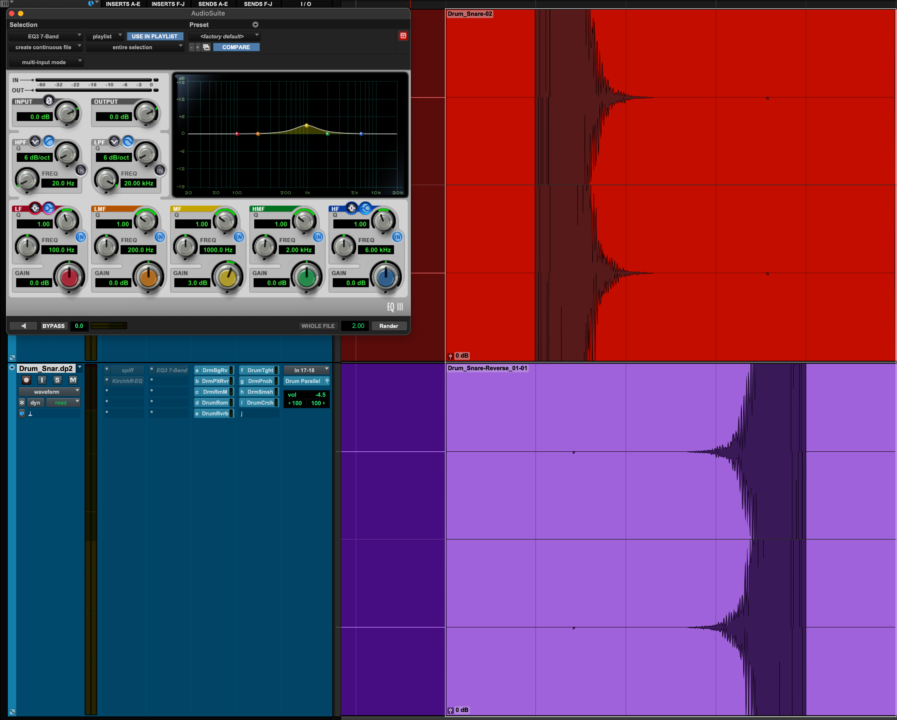
Forward-Backward 法は DAW 上でも、その概要的な再現はできます。

通常の Minimum Phase EQ や線形位相特性を持たないモデリング EQ などで処理したいトラックを複製します。
複製したトラックの時間軸を反転させます。Pro Tools であれば Audio Suite の Reverse プラグインが利用できます。
両方のトラックに同じ EQ 設定を適応させます。Audio Suite で実行すると簡単です。

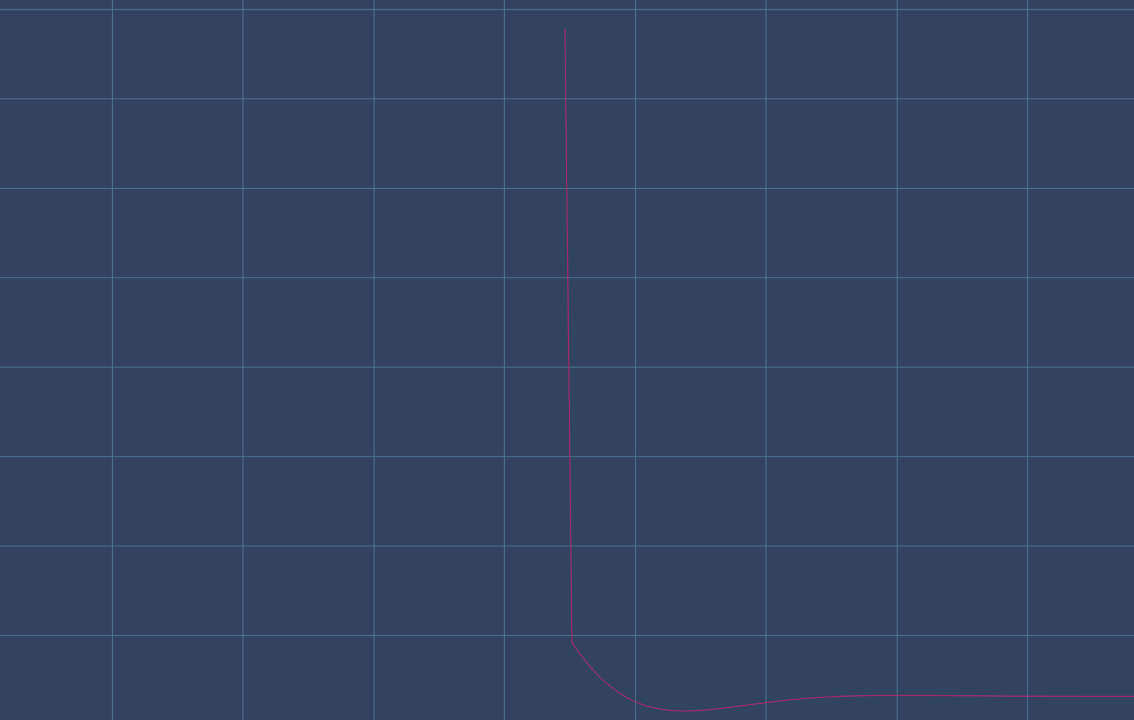
両トラックには同じ位相特性が付与されます。上記のような IR 特性が付与されます。

時間軸を反転させたトラックを正の時間軸に再度戻します。Pro Tools であれば Reverse をもう一度適応します。

反転したトラックの時間軸は正の向きに戻りましたが、フィルター特性の時間軸は反転しました。

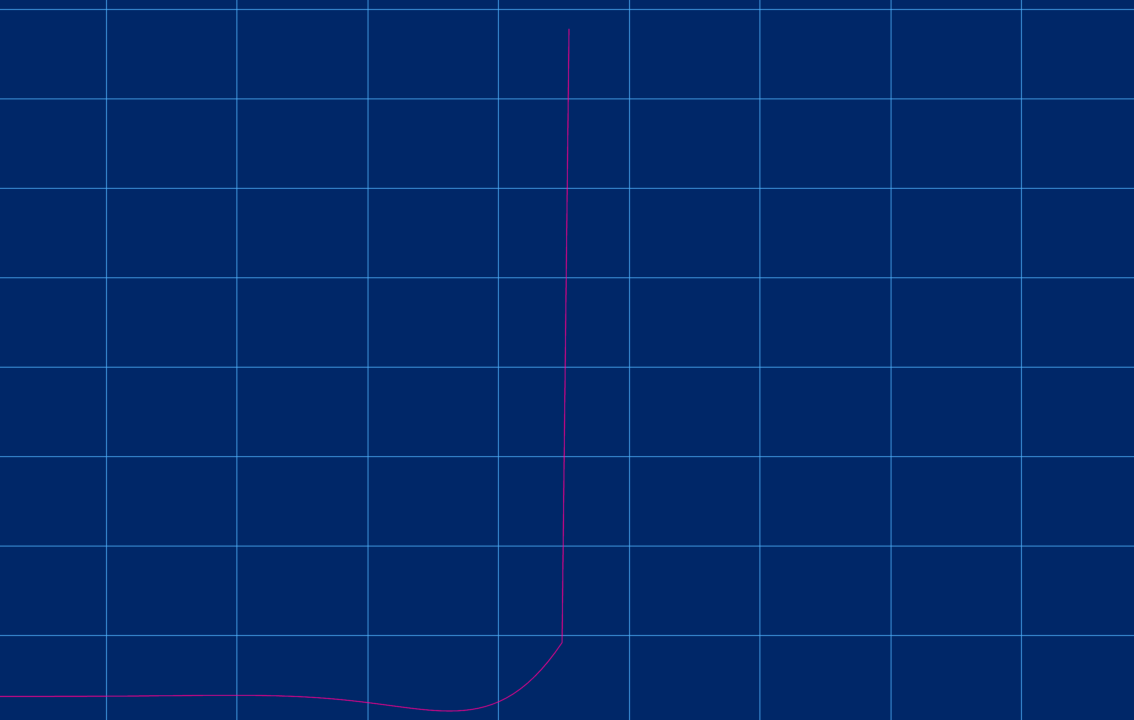
つまり、この (下側) トラックのフィルター特性が反転します。

これらが同時に発声した場合、位相特性は次のようになります。

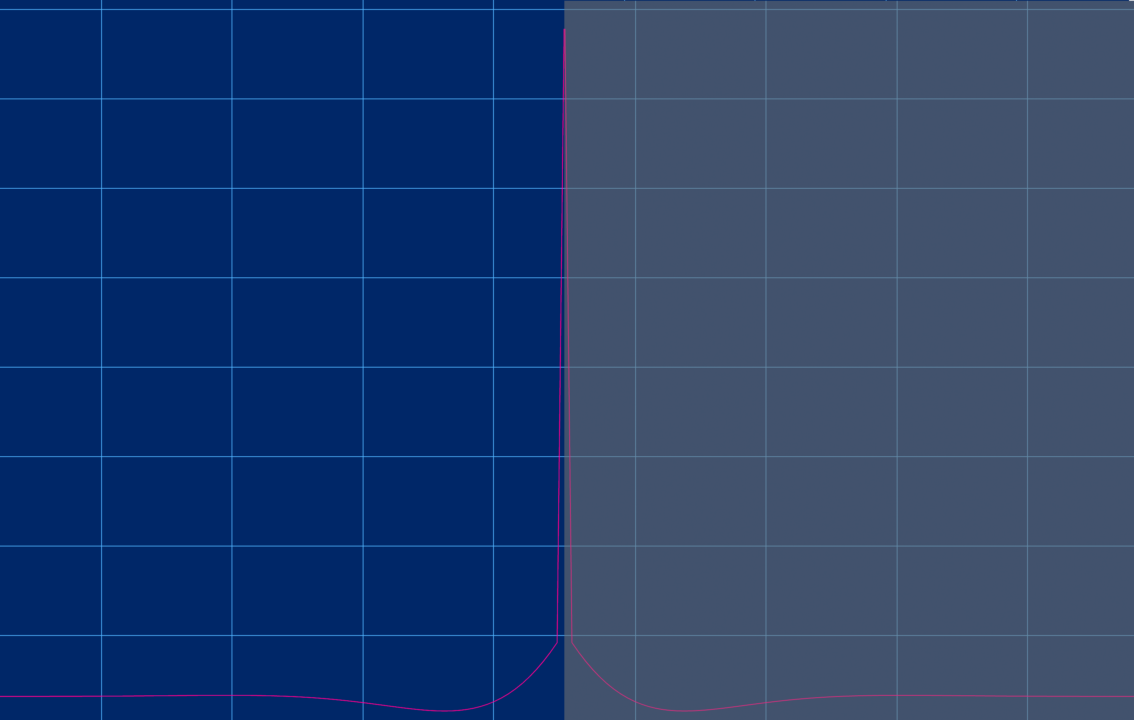
この原理を利用して対称性を DAW 上でも再現できます。これが Forward-Backward 法の簡単な説明になります。もちろん、これは IIR ベースの EQ を利用しつつ、Linear Phase EQ の特性を再現させる方法であり、実際にこれを利用すると振幅特性は単に倍になってしまうため、実際にはもう少し複雑な計算が必要であることは明白です。

もちろん、実際のプラグインの実装は Linear Phase EQ 同様に対称性の維持の影響により遅延が必要になります。

Forward-Backward Filter がすごいの？

違います。

オリジナルの Algorithmix LinearPhase PEQ orange の基礎構造とアルゴリズムが凄かったのです。

重要なのは基礎理論を応用した内部処理にあります。

本音を言うと、Algorithmix と MAAT はその革新的な内部アルゴリズムについては秘密であるため、どのような応用理論に基づいて thEQorange が仕上がっているのか、筆者にも当然わからない。

正直、評価する部分は、自身の音楽的感性には最終的には委ねられる。

内部処理は 80-bit で処理されている

内部の処理設計が優れているためにディティールに影響を与えていると MAAT は語る。

ちなみに Three-Body Technology の Kirchhoff EQ は内部 117-bit で処理できるモードがある。この MAAT EQ の内部処理と基礎的な考えは一緒なのだろうと思う。この 117-bit モードの影響は高精度の Linear Phase EQ モードなどを利用した場合に変化が観測できる可能性がある。がいずれそれを検証する時が来るだろう。

また、DMG Audio の EQuilibrium に関してはタップ数をかなり極限「262144」まで設定できます。

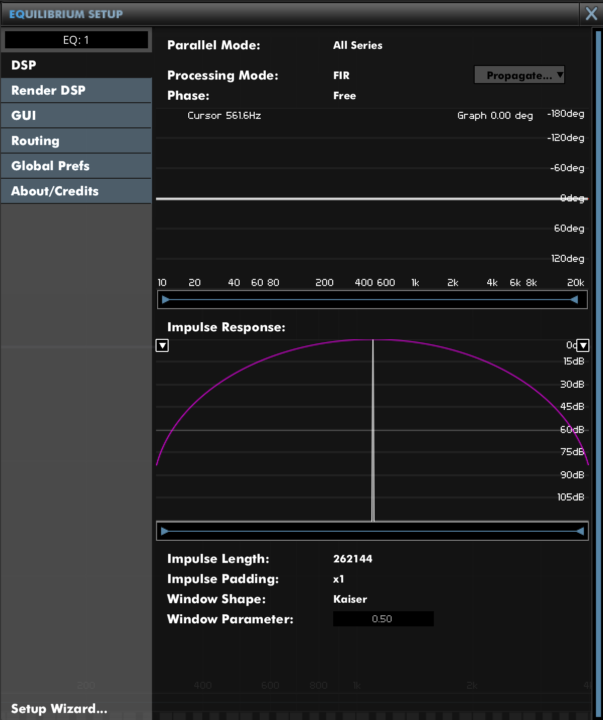
タップ数、ここでは Impulse Length という表記になっているが、この数値が高いほど、FIR のデメリットである周波数分解能、急なフィリタリング設定に於いて有意になる。これはサンプル数と同義で 262144 サンプルの Lookahead を行うよ、という意味でいい。

以下、タップ数の AI さんの回答。

Linear Phase EQ におけるタップ数は、そのデジタルフィルタの特性を決定づける重要な要素です。タップ数とは、フィルタを構成する係数（インパルス応答のサンプル）の数を指し、FIR（Finite Impulse Response）フィルタの設計に関連します。タップ数について詳しく説明します。

タップ数と周波数特性の関係: タップ数が多いほど、フィルタはより細かい周波数特性を持ち、急峻なフィルタリングが可能です。高いタップ数は、特に高精度で狭帯域のカットやブーストを行いたい場合に必要です。
遅延: Linear Phase EQ は、位相を線形に保つために遅延を導入します。この遅延はフィルタのタップ数に依存し、タップ数が増えると遅延も大きくなります。例えば、タップ数が 1000 のフィルタは、タップ数が 100 のフィルタに比べて約 10 倍の遅延を持つことになります。
計算負荷: タップ数が増えると、フィルタリング処理にかかる計算量が増加します。リアルタイム処理では、非常に高いタップ数は CPU 負荷の原因となるため、処理の効率化が必要です。
周波数応答の精度: タップ数が多いフィルタは、非常に鋭いカットオフ特性を持つことができますが、その分、インパルス応答のリップルが増えることもあります。このため、設計時には適切なウィンドウ関数を使用して、リップルを抑制しつつ、理想的な周波数応答を目指します。
最低タップ数の選定: 目的とする周波数特性やフィルタの性能に応じて、必要なタップ数が決定されます。例えば、低域を急峻にカットしたい場合には多くのタップ数が必要ですが、緩やかなシェルビングでは少ないタップ数でも対応できます。

タップ数はフィルタの設計全体に影響を及ぼすため、目標とするフィルタ特性や用途に応じた選定が重要です。

ちなみに PluginDoctor だと、極限のタップ数だと遅延が多すぎて、表示が一回りしてしまう。EQuilibrium の最大タップ数は測定が上手く表示されない。表示が二周しているということなんだが。

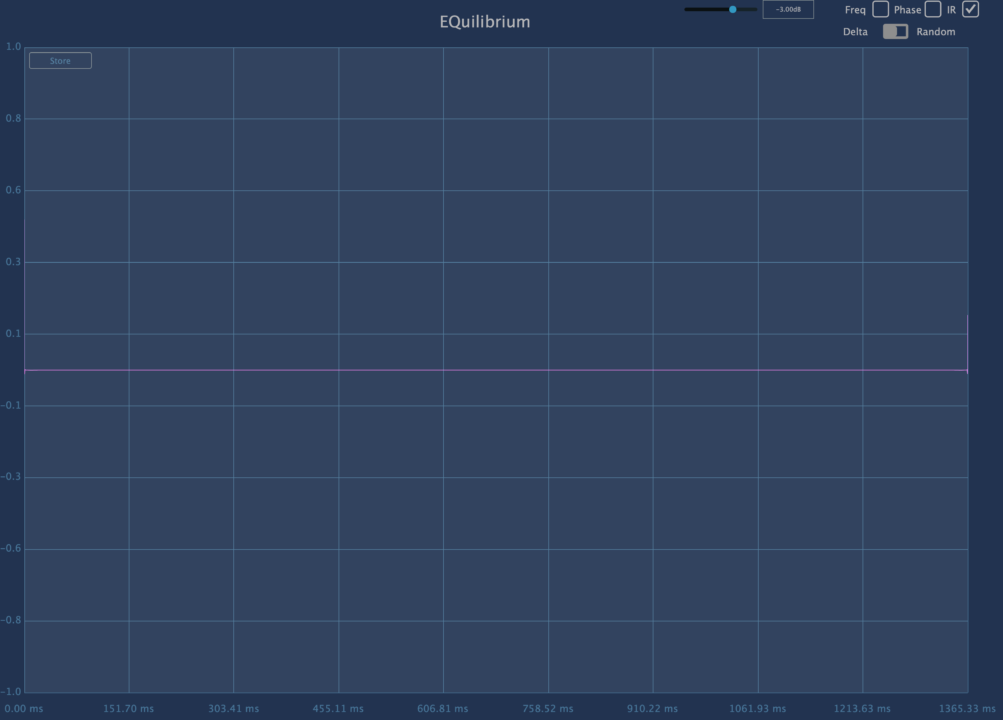
表示限界で、伝達特性が一回りして画面の左右端に表示されてしまう。

表示がおかしくなるので PluginDoctor でも正しい測定ができないプラグインもあるんだぜ。ということ。

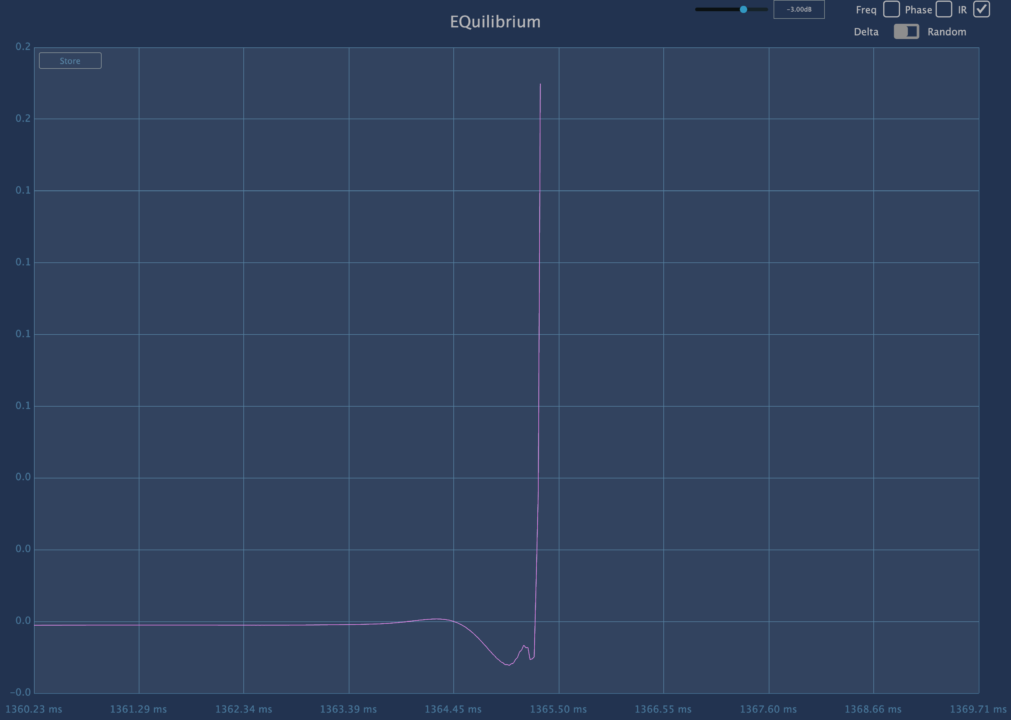
PluginDoctor で見れる最長のタップ数。48kHz のとき、遅延は 1365ms、約 1.36 秒となる。これはサンプル数に換算すると 48000 以上であるということ。であるが、実際はもっと遅延があるはず… 軽く計算すると 65536 っぽく、これは 2^16 に等しくおそらくそれ以上を測定できない。

通常、タップ数と遅延サンプルは同じになるため、この測定値が正しくはないのだが。正常に測定できていないのは間違いない。

thEQorage については DSP 解像度、内部の位相線形アルゴリズムの内部精度に関しては 4 つのステージがあるのみだが、xtra 以外利用はしないと思うレベルで動作は思った以上に軽い。もちろん遅延はあるし、もちろん処理が軽いプラグインではないが、最近の高性能プラグインと比べたらリアルタイム処理に問題が起きるほどではないと思うし、普通に動作は軽い。

すぐに評価を測定値に頼るのは辞めてほしい

こういうサイトを運営していたり、動画を制作しているとすぐに PluginDoctor の測定値を図って議論しろ、測定値を分析して解説しろ、という方がいますが、そもそも測定値で議論できるほど、あなたは網羅的な知識や理論的な構造を理解しているのですか？と問いたいです。

測定値がすべてであるのであれば、何故、数学的に忠実でスペック的に最強の EQuilibrium が日本で一番流行っていないのでしょうか？

測定値はあくまで測定値が得られるだけであって、実際の過渡特性と出力音が一致しないことは、世界トップレベルの頭の良い音響エンジニアリングの猛者が証明しています。

僕達は別に測定をしているエンジニアでもなく、理論的な出力値を求めているわけではありません。如何に音楽的に処理ができるのか、というところしか求めていません。

殆どの場合、測定値は自分の利用に対する指針は得られますが、他人に対する説明には全く使えません。

もちろん、thEQorange で達成できない音像があった場合、EQuilibrium で達成できる可能性がある。この違いは測定値の違いではなく、単に求める音の出力結果違いでしかなく、それは後付けで理論的に説明できる可能性はあるが、視聴者などに対して論理的に判断して EQ を選択することを測定から絶対に説明できない。なぜなら、視聴者自身が求める音がなにか、は私は論理体系化できなからだ。

正しい測定評価は知識がないと難しい

幾度となく説明してきたが、そもそも測定値を正しく評価するのは熟練のエンジニアでも難しい、というか普通のエンジニアは無理、というレベルで測定に関する知識は持ち合わせていない。エンジニアは耳を頼りに、時に測定して問題の特定を行うが、世の中のほとんどの情報が測定結果の評価を間違えている。測定は欲しい結論のために行う人が大多数だからだ。

測定結果を疑うことをしない人も多い。

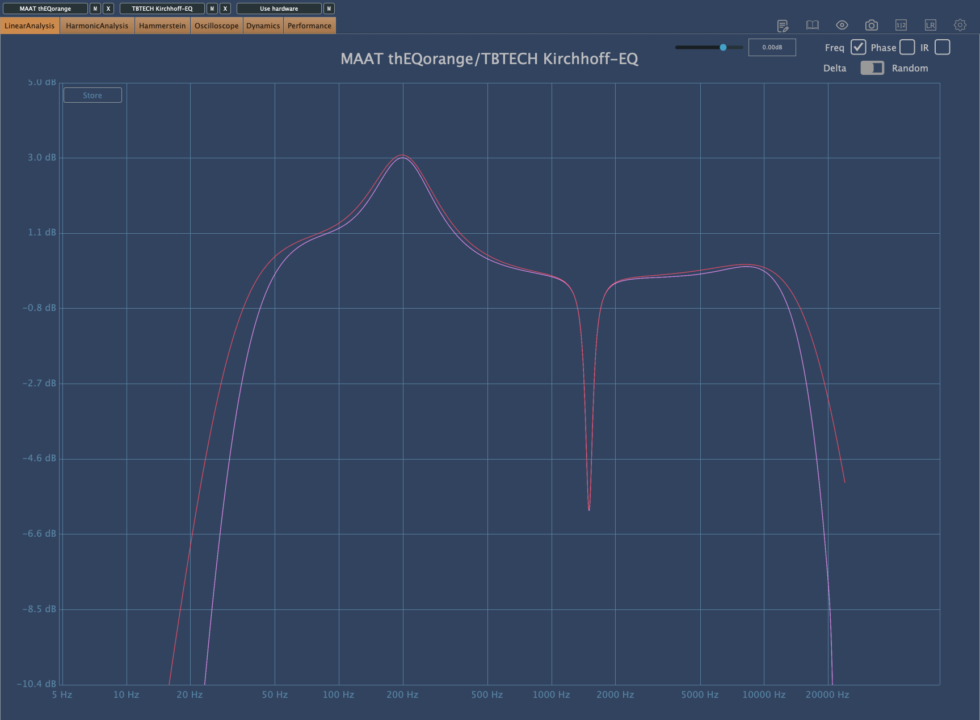
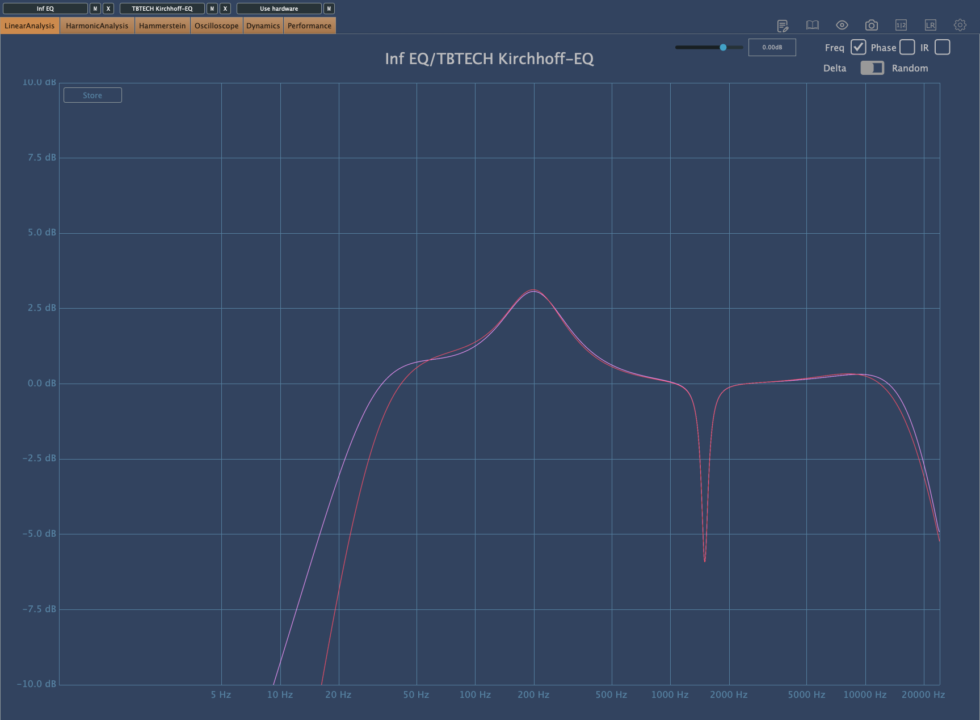
上記は Kirchhoff EQ と thEQorange の周波数特定を見ている。同じ値で同じ EQ を実行しているが、Q の係数を一致させることはできない。これは設計により変動するからである。この事実を知っている人がまず、どれだけいるのか、疑問である。EQ は Q の品質係数が異なるため、厳密な評価は事実上不可能である。ただし、比較評価には十分であると結論付ける。

上記は Phase Shift の評価を見ているが、どちらも全く変化がない。非常に細かく見るとその他の EQ にも見られるリップルが僅かに観測できる。そしてこれが thEQorange のアルゴリズムの IIR ベースと Forward-Backward 法の両立による高域特性のアルゴリズムの根源となる動作であり、実質的に意味のない測定になる。そもそもこの場合では実用的には基本無視できる値であるため両者測定値は全くの互角。

もちろん、thEQorange は既存の再帰フィルターベースの Forward-Backward 法を応用したアルゴリズムであるため、極端な LPF を行えば測定値が悪くなることは私は知っているが、それが EQ の独特の音質評価の根源であり、そこに対する評価を正しくできない人が見たら測定値が悪いので音が悪いなどと判断する。音を聴いてもいないで評価する典型。

それはそもそもの製品の評価と使い方を間違えていると言わざる終えない。そういう設計であるからだ。そもそも測定値が悪くなるプラグインなぞ腐る程あり、しかも殆どの場合、想定外の使い方による特殊な例を持ち出す輩が大半だ。測定値と出力結果を正確に結びつけられないのは単なる個人の知識レベルの問題や業務的な有無レベルの問題になる。

つまり測定結果からは基本なにも得ることができない。別に測定値が悪いことと、音の評価は一致しないことを世界のトッププロは知っている。だから音を聴くしかない。なぜなら最終的なアルゴリズムの調整は世界中のトッププロが評価しているためである。測定値を重視してアルゴリズムを設計していない。これは私が今まで紹介してきたプラグインも同様であり、測定すると全く評価的にはダメダメなものを紹介している。

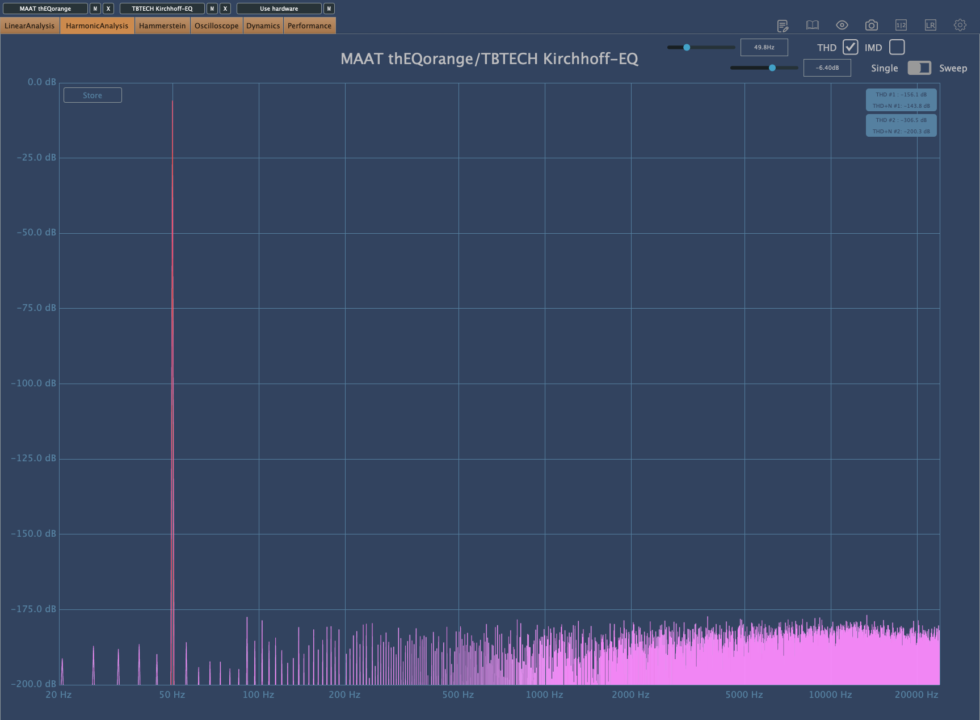
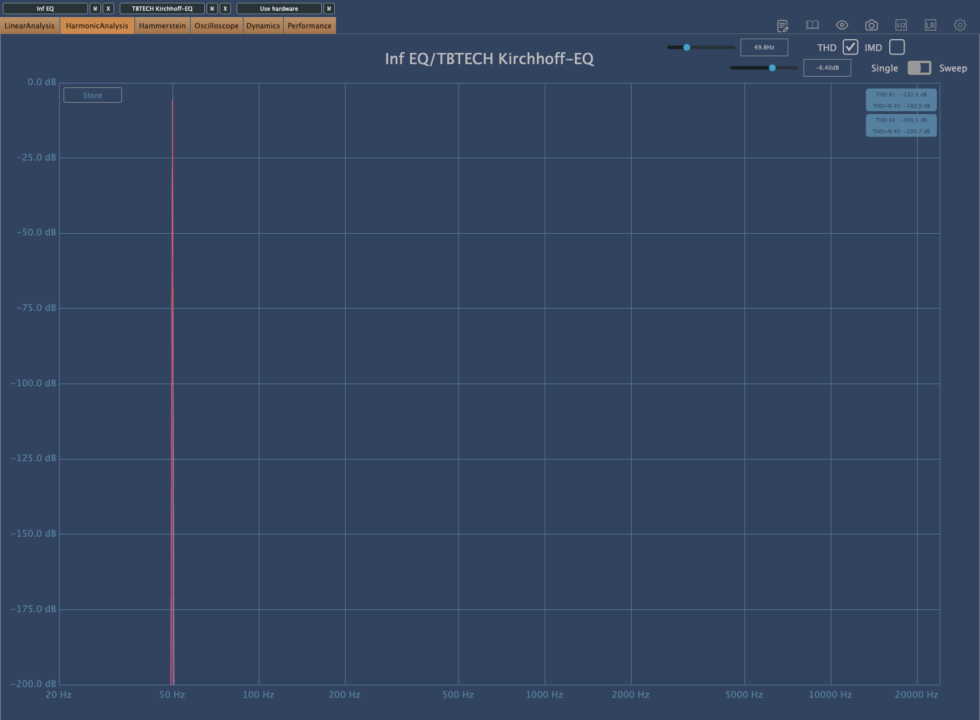
これはシステム上の THD の評価値。そもそも実用上の 24-bit DA の下限以下であるため、こちらも両者測定値の意味をなさない状況で優秀である。設計が新しい Kirchhoff EQ の方が測定値的には優秀であるが、このノイズは可聴範囲に影響を及ぼすことは極めて考えにくく、これが直接評価に影響しない、または影響を及ぼす場合にも、デメリットにはなり得ない。

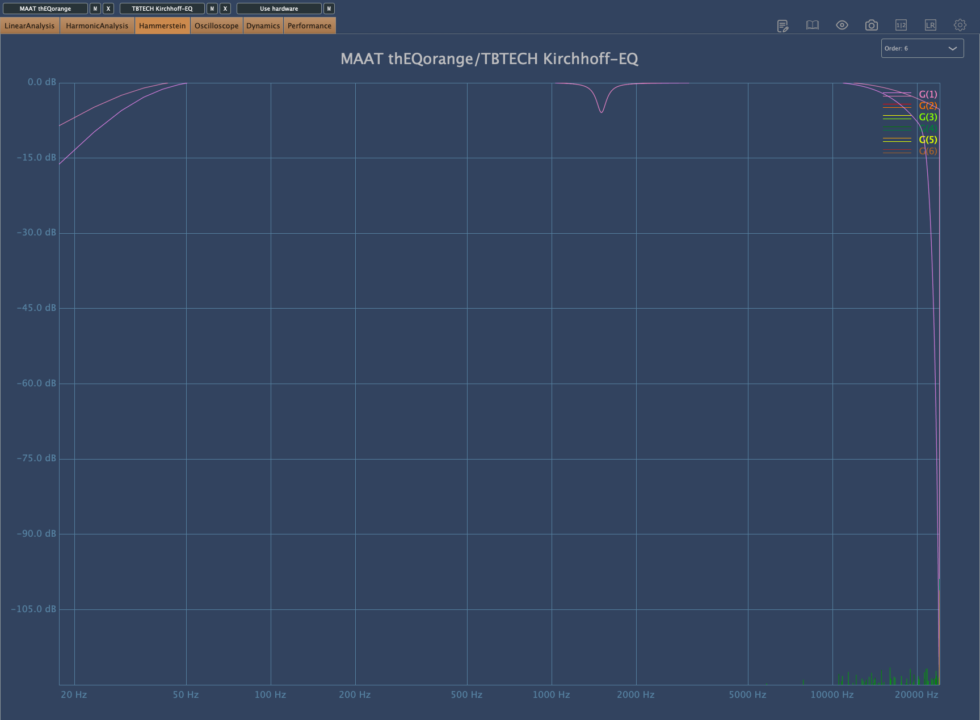
こちらは Hammerstein の評価で周波数ごとの高調波の評価である。こちらも両者全くと言っていいほど同じレベルであり、評価の対象にはならない。そもそも下限以下である。一つ言っておくと、Kirchhoff EQ の方がナイキスト周波数内において雑音が集積しており、測定に於いてある一点がオーバーフローしているように見える。

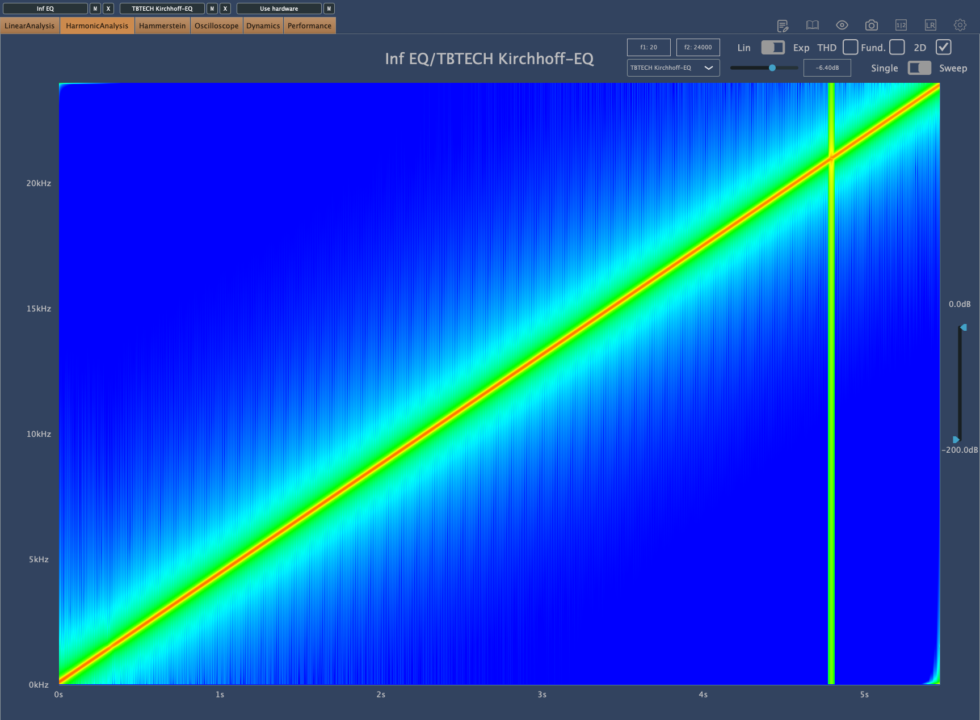
Sweep 測定をするとありえない観測結果が得られる。これをそのまま信じるのであれば、Kirchhoff EQ は欠陥だ、と高らかにいうユーザーもいるであろうが、この測定結果が実際に実用で発生する問題なのか、測定が信用できるのか、はまた別の問題になる。この測定値は他のプラグインでもよく発生するナイキスト周波数内での雑音集積問題であるが、おそらく遅延に関連する測定のバグか、または実用上は無視できるので意味をなさない測定であると私は結論づける。

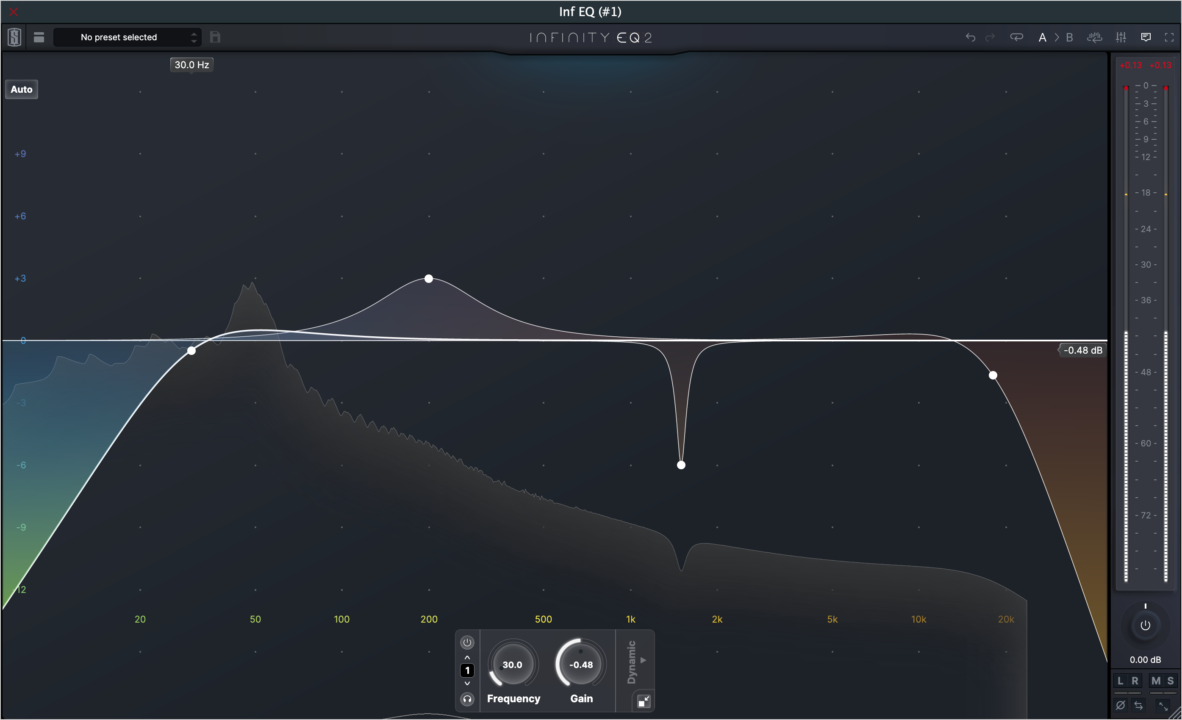
ちなみに、最近 Ver2 がでた Infinity EQ2。

これは名前が Infinity であるので簡単に想像できると思うが IIR Filter ベースの極限 EQ であり、全く日本では話題にもなっていないが、設計は明らかに異常というか素晴らしいことが測定からわかる。

残念ながら Q 係数の設計が独自すぎるので Q をほぼ同じように設定できないので厳密な評価ができているとは言いづらいが、十分許容範囲であると思う。

この EQ は名前が Infinity EQ2 であり、名前の通り、Infinite Impulse Response Filter ベースの EQ であるため、Phase Shift を理論的に起こす。

ただし、雑音の評価は Kirchhoff EQ にも負けず劣らずで、Infinity EQ2 は遅延が 0.02ms であるが、Kirchhoff EQ は 682.64ms である。実用を考えた場合、どちらが優位か、はその状況で変化してしまうため、そもそもこの2つの EQ を測定で評価しようとすると、同じ土俵 (実用的な視点) で評価するのは無理といってもいいレベルである。

そして、Hammerstein の評価も同じであるが、一点違うのは以下の画像評価。

ちなみにこの Infinity EQ2 の音質評価をしている人を僕は日本語で見つけたことはないが、非常に音が硬いと言うか、今までの IIR フィルターベースの EQ に比べて明らかに音が鈍らないし、他の EQ でなんか音が柔らかくなりすぎる時にこちらを選択すると別の音が聴こえてくる。

Infinity EQ2 はナイキスト周波数内での雑音集積がない。おそらくこのプラグインは内部的にオーバーサンプリング等が実装されていない所以、おそらく遅延絡みだと思うが、実際のところ正確な理由はわからない。

これをもって評価をするのであれば、Infinity EQ2 は測定で問題が発見できなかったので Kirchhoff EQ よりも優秀であると結論付ける極端な例が世の中には存在する。実際には Kirchhoff EQ には欠陥がある訳ではないが、その優劣を正しく評価されないのは測定側の都合である。

これはそもそも、評価を正しくできない人が測定を行い、その測定結果を元に持論を展開するだけで、実用上、意味のない測定結果を元に結論を導き出す例は世の中には非常に蔓延っている。

thEQorange は通常の Linear Phase EQ とは運用が異なる

通常の Linear Phase EQ は位相変形を排除しつつ、最後の微調整に使うものである。と動画上でも大体の大筋として語っている。もちろん、積極的な EQ にも使えるが、それはあくまで Linear Phase EQ のメソッドの範囲内の話である。

しかし、この thEQorange に関しては、どうしても Linear Phase EQ のセオリーを逸脱した EQ を Linear Phase EQ で行いたい場合や、最後の調整で積極的に HPF や LPF を使いたい人向け。

FIR フィルターベースの Linear Phase EQ では、精度が足りないと、どうしても LPF を行ったときに音が訛ったり、リンギングやエコーの問題が聞こえる場合がある。ここではリアルタイム性も重要な要素になる。もちろん、コストが許すのであれば、EQuilibrium を極限設定のほうが、測定値的には絶対に thEQorange は勝てないはずだ。

しかし、この EQ であれば、積極的な EQ 設定を Linear Phase で行えるし、Linear Phase EQ の HPF、LPF をリアルタイムで実行できる。極限タップ数ではリアルタイム利用は現状不可能である。

また、公式的はマスタリングステージにおける外科的な EQ に使え、基本的にマイナスゲインでの運用を推奨している。